本文为中国激光第3147篇。
欢迎点击在看、转发,让更多人看到
文中图片均为李俊昌教授原创,版权归作者所有。
作者 | 昆明理工大学 李俊昌
引文
2017年,光学名著《傅里叶光学导论》第4版对柯林斯积分作了介绍[1]。柯林斯积分也称柯林斯公式,是计算光波通过傍轴光学系统的衍射计算公式。在应用研究中,当初始平面的光波场的空间变化率不高时,柯林斯公式可以足够准确地变换为由菲涅耳函数表示的计算式[2],而菲涅耳函数可以足够准确地用代数式快速计算。用菲涅耳函数计算柯林斯公式的研究具有实际意义。
本文介绍两种不同的菲涅耳函数计算公式:其一摘自美国学者A. E. Siegman的专著《Lasers》[3],其二是作者导出的计算公式[2]。我们将对两种菲涅耳函数的计算公式精度进行比较,并给出用菲涅耳函数计算柯林斯公式的一个激光工业应用实例。
最后,通过菲涅耳衍射积分的研究,导出采用菲涅耳函数计算一些特殊衍射问题的计算公式及相应的实验证明。
- 01 -
老师给的研究任务
提前回到学校的彭颖与师弟黄金鑫和师妹赵雯丽商量后,通过两天努力,在师弟和师妹的协助下,开学前完成了她期望进行的彩色数字全息实验。正当他们为得到满意的实验结果而高兴之时,没注意樊老师进了实验室。
“小彭,你们的实验怎么样?”
“啊!樊老师,还不错,托师弟和师妹之福,今天光路调整很顺利。”彭颖回答后,请樊老师到电脑前坐下,在电脑前给樊老师展示了她根据全息图重建的彩色图像……
看完实验结果后,樊老师站起身说道:“实验非常不错!今天我想让你们做一项有意义的工作。”说着,面向几位研究生拿出他带来的一本书。
樊老师说道:“你们今后的研究课题都涉及衍射数值计算。目前,衍射的数值计算基本上采用快速傅里叶变换 (Fast Fourier transform,FFT),但是,在这本书中有衍射调制函数法计算衍射的方法。由于该方法只涉及菲涅耳函数的计算,书中导出了菲涅耳函数的近似计算公式。在你们熟悉FFT算法之前,为加深对菲涅耳衍射积分的理解,我与小彭的指导老师商量过,请小彭帮忙,让你们两人进行一点研究工作。”
樊老师将所带来的《激光的衍射及热作用计算》[2]一书交给赵雯丽,接着说道:“这本书现在已经买不到了,现留给你们,以后还给我就行。我想让你们做的工作是:
一、将书中衍射调制函数法计算衍射的公式改写为能用于直边衍射、狭缝衍射及圆孔衍射的计算式。
二、进行理论计算与实验测量的比较。
三、通过数值计算理论或实验,考查书中菲涅耳函数计算公式的可行性。”
说完后,樊老师又补充道:“在实验室进行直边衍射、狭缝衍射及圆孔衍射等实验很容易。通过理论计算与实验测量的比较,可以加深对菲涅耳衍射积分的理解,对你们今后的深入学习算是一个热身。”
彭颖是宋老师的研究生,听完樊老师的话,她立即作了回答:“没问题的,樊老师。我已经有这本书,我看过书中的衍射积分在空域计算这一章,但还没有实际应用过。现在,我们基本都用后来李老师和熊先生写的《信息光学教程》第2版[4]提供的FFT计算程序计算衍射了。”
“谢谢小彭!”针对所做工作的意义,樊老师再补充说了一些话后,便离开了实验室……
樊老师走后,彭颖与师弟师妹进行了讨论。按照讨论结果,黄金鑫负责任务一,即导出用菲涅耳函数表示的直边、狭缝及圆孔衍射的计算式,樊老师留下的书先让他看。
对于任务二,他们三人搭建的三种色光照明的彩色数字全息光路还在,实验室有准确知道直径的钢丝及圆孔光阑,只要关闭两种色光,遮住剩下一种色光的参考光,便能用CCD记录下不同遮挡物的衍射图像,可以很快做实验。
在讨论任务三时,彭颖说:“我本科学习的《信息光学教程》中[4],有另外一种菲涅耳函数的近似计算公式,书中给出的参考文献是Siegman的专著 《Lasers》。顾德门的《傅里叶光学导论》第4版介绍柯林斯公式时,这本专著还是参考文献呢。看来Siegman是一个知名的光学专家。不妨同时用这个公式及李老师导出的公式进行衍射计算,然后与实验研究进行比较,这样则能知道两种公式哪一个更精确。”
“我来做这件事吧。”赵雯丽自告奋勇地说她来完成这项工作,并且补充说道:“师姐,菲涅耳函数的数值计算用MATLAB编程很方便,既然你能找到另外一个菲涅耳函数的数值计算公式,我觉得可以将MATLAB编程计算的结果作为准确值,理论上考查李老师及国外学者导出的公式的误差,这在理论上更能说明问题。我不知这个意见是否恰当?”
“当然好!我在《傅里叶光学导论》第4版中就看到菲涅耳积分可以通过查表或MATLAB计算。”彭颖同意后,接着又说:“我们三人建一个微信群吧,这样便于交流。”
建好微信群后,他们征得樊老师的同意,请樊老师也入了群。
三人立即开始任务二的实验研究,并记录下相关实验结果……
- 02 -
菲涅耳函数的两组近似计算公式
当天晚上,彭颖便在《信息光学教程》第2版中找到Siegman给出的菲涅耳函数近似计算式。于是,她发了下面微信。
菲涅耳函数由下面两积分定义:
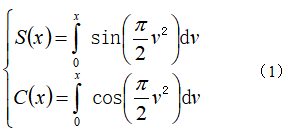
两式只能求数值解,估计国内外存在不同形式的近似计算式。Siegman在其专著《Lasers》中给出的菲涅耳函数的计算公式在《信息光学教程》第2版的第2章有介绍。该近似式是:
其中,
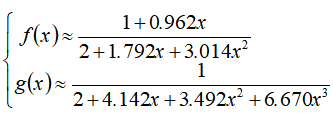
李老师导出的计算式是[2]:
基于菲涅耳函数的计算公式,《激光的衍射及热作用计算》第3章介绍了初始平面是一个矩形孔时光波通过由2×2矩阵元素
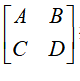
描述的光学系统衍射的计算方法。对于衍射距离为d的衍射计算问题,对应的光学矩阵可以简化为
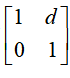
。因此,只要令书中公式中的A=1、B=d、C=0以及D=1便能进行樊老师让我们做的工作。最重要的是导出的公式要与实验测量作比较。
根据我们所做的实验,因照明光已经较好地扩束和准直,可以将照明光视为均匀平面波。此外,由于我们用CCD记录的是衍射场的强度图像,目前只需要导出形成能计算衍射场强度的公式。
- 03 -
两种菲涅耳函数计算公式的精度比较
没想到,赵雯丽第二天便得到结果。她用已经比较熟悉的MATLAB软件通过积分语句来计算菲涅耳函数,并以此为标准,考察了A. E. Siegman及李老师的近似公式的准确性。研究结果表明,两种公式具有基本相同的精度,从严格的理论意义上看,李老师的近似公式的精度还略胜一筹。于是,她发了下面的微信。
樊老师及师姐师兄:
我用MATLAB编程比较的结果表明,A. E. Siegman及李老师的近似公式具有基本相同的精度。但从严格的理论意义上看,李老师(LIJC)的公式要更好一些。请看比较结果。



图1 C(x)曲线的MATLAB积分运算与两种计算公式的比较



图2 S(x)曲线的MATLAB积分运算与两种计算公式的比较
从以上两图比较可以看出, 除了Siegman公式计算S(x)时在零点附近出现微小负值,与菲涅耳函数的定义不附外,两种计算公式的计算曲线相近,很难看出区别。
我是用MATLAB2014版计算的。Siegman公式用时0.344627秒,LIJC公式用时0.333319秒,MATLAB积分运算用时0.761707秒,MATLAB积分运算用时最多。
为进一步作定量比较,以下两图分别给出两种计算公式的计算值与MATLAB积分运算值的差值曲线。在图中,我标注了在0~3π计算范围两种计算公式的平均绝对误差。
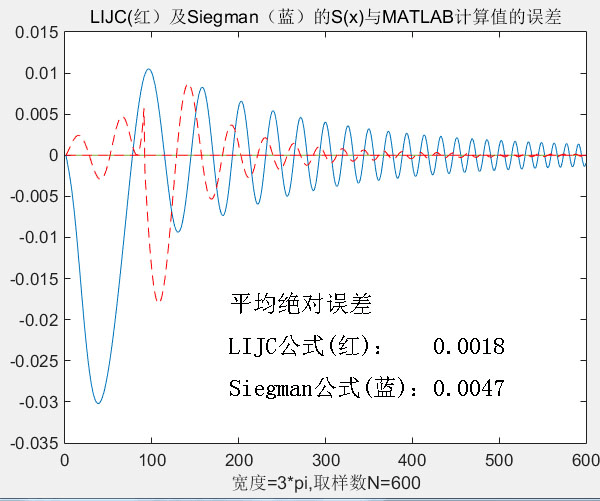
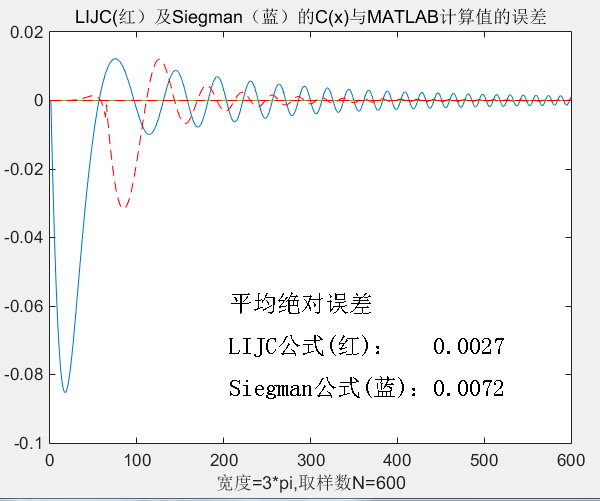
图3 LIJC公式与Siegman公式计算值与MATLAB积分运算值的差值曲线
应该说,LIJC公式相对于Siegman公式要更接近MATLAB的积分运算值。
- 04 -
菲涅耳函数的改进计算式
收到微信的樊老师对赵雯丽的工作很满意,次日回信告诉大家:
小赵进行的理论研究很好!昨天我在学校遇到李老师。当我说到你们的工作时,李老师非常感兴趣。他说,二十多年前他曾经利用他导出的菲涅耳函数计算公式去解决过许多实际衍射计算问题,特别是能用于实际激光热处理中曲面工件表面的衍射场强度快速计算,由于得到与实验非常接近的结果,便将其写在《激光的衍射及热作用计算》一书了。现在,《傅里叶光学导论》第4版中,顾德门教授将菲涅耳函数称为菲涅耳积分,并且指出,其计算可以通过查表或MATLAB等软件计算。李老师认为,由于菲涅耳函数在衍射计算中的重要性,如果有一个计算公式能快速准确地计算无疑是重要的。但是,他以前导出的公式与Siegman公式究竟哪一个更准确,他还未进行过比较。看到你们的研究结果让他非常高兴,现在他觉得心里较踏实了。
没想到,今天早上我收到李老师的微信,原来,李老师昨晚仔细研究赵雯丽的C(x)与S(x)计算值与MATLAB积分运算值的差值曲线后,觉得在x≤2区间对菲涅耳函数用 “牛顿——科茨”数值积分公式表示后,可以到精度更高的表达式。虽然形式上略复杂,但编程计算时间仍然略低于Siegman公式。
李老师将菲涅耳函数的计算式更新为


按照改进后的公式,在0~3π计算区重新得到下面的图像。


图4 改进后的LIJC公式与Siegman公式计算值与MATLAB积分运算值的差值曲线
通过改进后,新的LIJC计算公式与MATLAB积分运算值的差异更小了。
- 05 -
菲涅耳函数的应用实例
樊老师在微信中接着说,采用菲涅耳函数快速计算衍射是20世纪末李老师在法国进行红外强激光热处理合作科研中提出来的。因李老师提出的矩形均匀激光斑叠像器能将激光光束聚焦为方形均匀光斑[5],并且该光学系统的主体可以通过水冷应用于工业大功率激光热处理生产线,后来在法国用于提高汽车零件的激光热处理质量的研究,取得很好的成果[6-7]。在实际研究过程中发现,由于材料的热扩散作用,获得均匀的材料表面的激光扫描强化层时并不需要激光是均匀分布,而是在垂直于扫描方向两侧较强的马鞍形强度分布,具体分布还取决于扫描速度及材料的导热性能。为定量研究这个问题,通过热传导理论及铁基材料的马氏体相变理论的学习,李老师在理论上导出当扫描工件为平面时,获得一个均匀相变层时扫描光束的强度分布形式如图5所示[6]。
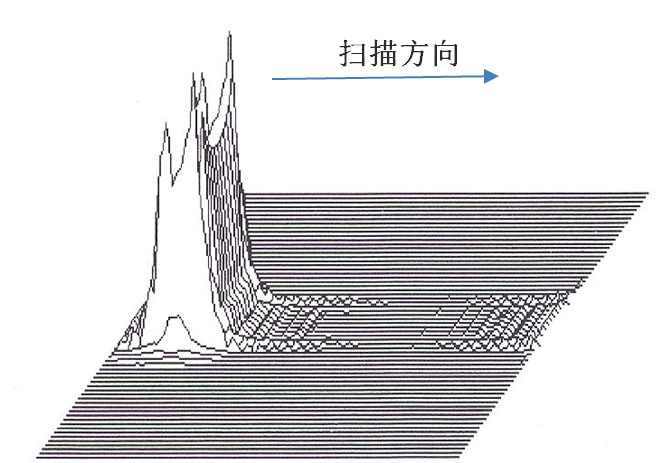
图5 获得一个均匀相变层时扫描光束的强度分布形式
值得庆幸的是,李老师所设计的光学系统经过简单调整就能够将高斯光束变换为这种马鞍形强度分布[5-6]。然而,实际激光热处理工件表面通常不是平面,为便于根据光斑强度及时调整热处理工艺,原来只计算光学系统中理想叠像平面光斑强度的理论公式不再适用,需研究任意给定调整状态及任意给定热处理表面光强分布的快速计算式,才能为后续的热作用计算及热处理工艺制定提供依据。为此,李老师基于柯林斯公式对光学系统导出由菲涅耳函数表示的计算公式,该公式可以计算到达任意曲面上的光强分布。但菲涅耳函数的计算非常繁杂,为实现快速计算,通过认真研究,才导出这个足够准确的菲涅耳函数代数运算式。这些工作,为光学系统的实际应用提供了很大的便利。
图6是1993年发表于法国物理杂志的一篇论文上该光学系统用于实际激光热处理取出的实验研究图像[7]。
(a)扫描面为平面

(b)扫描面为旋转曲面
图6 光学系统用于不同形式工件表面扫描处理后的相变硬化带剖面金相照片
其中,图6(a)是让该光学系统变换的马鞍形激光斑扫描时,平面铁基材料获得均匀相变硬化带剖面的金相照片;图6(b)是用该光学系统处理汽车曲轴的旋转形凹曲面模拟试件的相变硬化带剖面的金相照片。可以看出,非平面的工件也能够通过该光学系统变换后的光斑扫描得到均匀的相变硬化带。
在回顾这一段历史时,李老师表示,许多科学研究课题是在应用研究中逐渐形成的,实际遇到的问题往往需要多学科交叉的理论知识才能解决。基于自己熟悉的理论,在应用研究中认真再学习新理论,研究新问题,根据实际需要扩展自己的知识面,才有可能取得研究成果。
- 06 -
几种特殊衍射问题的计算公式
看过樊老师发来的信息,黄金鑫阅读了《激光的衍射及热作用计算》第3章,特别认真地读了该章第3节菲涅耳衍射调制函数的讨论。虽然大学本科学习中未见到过柯林斯公式,但他将A=1、B=d、C=0以及D=1代入柯林斯公式即得到已经很熟悉的菲涅耳衍射积分。根据这一节的学习,他已经知道第3节的主要内容是:当光学系统初始平面是给定复振幅的光波照明矩形孔时,可以利用菲涅耳函数近似计算光波通过光学系统的衍射场。
总结两天以来的学习心得,他在微信群中发了下面的微信:
我已经看懂《激光的衍射及热作用计算》书中是如何利用菲涅耳函数来计算光波通过光学系统的衍射了。近似计算的思路是这样的:在衍射空间建立直角坐标系O-xyz,令光轴与z轴重合,将初始平面的光波场分解为若干小的方形或矩形区构成,让每一小区域的边界分别与坐标x,y平行。此后,将每一小区域的光波场按照泰勒级数展开,略去二次以上的高次项后再代入柯林斯公式,则可以形成由菲涅耳函数表示的计算每一矩形区域光波通过光学系统的计算式。按照线性叠加原理,对初始平面上每一矩形区域的衍射场叠加,则可以获得初始平面是任意透光孔时观测平面的衍射场。虽然用FFT计算效率较高,但计算是对二维观测平面上的所有点进行的,利用菲涅耳函数计算时可以对任意给定的观测点作计算。正如樊老师微信说的,如果观测面是曲面,这种算法有实际意义。
若菲涅耳衍射距离为d,将A=1、B=d、C=0以及D=1代入书中计算公式,并根据光阑的性质,设计不同边长及中心位置不同的矩形孔,便能得到用菲涅耳函数表示衍射场的计算式。下面是我得到的几个特殊衍射计算公式:
1)直边衍射计算公式
半无限大体直边衍射可以视为边长足够长,但中心远离光轴的矩形孔的衍射。令,为光波长,矩形孔的一个边与y轴重合,透光孔在x轴正向,均匀平面波照明的直边衍射场复振幅公式是
衍射场强度分布则为
2)狭缝衍射计算公式
设矩形孔横向宽度为2L,纵向高度足够长,中心在坐标原点,狭缝衍射计算式为
式中,
衍射场强度图像则为
3)窄带衍射计算公式
利用巴比涅原理,横向宽度为2L窄带衍射计算公式可以利用(7)式写为
衍射场强度图像则为
4)任意形状孔的衍射计算
我觉得将圆孔视为大量小矩形孔的组合虽然可以用李老师书上的公式计算,但比较繁杂,而将菲涅耳衍射积分近似变为二微求和运算就比较简单。这样,设任意形状的孔S可以由N个中心坐标为(xn,yn)的小方形孔足够好地拼接近似,设小孔边长为Δ,菲涅耳衍射积分可以近似表示为
强度分布则为
该式能计算任意复振幅分布U0(x,y)的照明光通过任意形状孔S的衍射计算。对于圆孔衍射,若照明光是圆对称分布,只需要计算沿x或y正向的一些点,最后便能用程序综合出衍射场。
以上是我的学习结果。如果无问题,我就开始编写程序,并用我们的实验来验证这些结果。
很快,彭颖在微信群中给出回答:“师弟的理论公式应该没有问题,编写程序吧!看看是否能与实验测量相吻合。但应该注意的是任意形状孔的衍射计算的公式(11)的计算时,要让计算宽度L及取样数N满足L=λd/Δ。”
“为什么?”黄金鑫很快提问。
“我会在微信中发另一个文件说明这个问题。任意形状孔的衍射计算的公式(11)与我认识的两个大学本科的好学生不久前给我说的菲涅耳微波元法很相似。”
很快,按照专栏文章8的讨论,彭颖给师弟和师妹发了微信,并特地向他们介绍了现在北京两所名校上本科的尚进和郝思。
- 07 -
特殊衍射问题计算公式的实验证明
很快,黄金鑫用MATLAB编写了计算程序。理论模拟与衍射实验测量的比较表明,采用Siegman公式或李老师的公式,均能得到与实验测量很吻合的结果。
为尽快将结果告诉两位同窗,他在微信群中发了消息后,立即给彭颖打了电话。
彭颖回电话给他,要他来实验室,因为她和赵雯丽都在实验室里,让他直接在实验室的微机上给他们演示计算结果。
很快,黄金鑫到实验室展示了他的计算图像。

“你们看!我先将圆孔衍射的理论计算及实验测量的比较图调出。理论计算与实验测量吻合非常好。”黄金鑫边调出实验图像边进行解释。
(一)圆孔衍射的菲涅耳波元法计算
圆孔衍射的计算,由于圆对称性,只需要按照公式(11)进行x轴正向一序列点的衍射场强度计算,便能综合成二维平面的衍射场。我们做的实验是直径1 mm的孔经过距离10 m的衍射,衍射图像远大于CCD的窗口,衍射斑是用手机拍摄的。我在手机拍摄图像上选择宽度L=6 mm的区域作为实验比较图。按照L=λd/Δ的公式,由于我们实验用的激光波长是0.000632 mm,可以求出Δ=λd/L=0.1 mm。选择N=L/Δ=600进行计算。由于照片中央斑的强度过饱合,在模拟计算时,我在模拟计算时将归一化强度大于1/20的区域均视为1进行显示,这就是实验测量与理论模拟的比较。

图7 菲涅耳波元法实验证明
(二)直边衍射公式的实验证明
“下面分别给出CCD测量的不同衍射距离的直边衍射场强度与两种公式计算的理论模拟的比较图像,图像宽度均为6 mm。”
衍射距离200 mm的直边衍射实验测量与理论模拟的比较图如下


(图像宽6mm)
图8 衍射距离200 mm的直边衍射测量图像与理论模拟图像比较
在理论模拟图中,我用绿色线标出了观测平面模拟研究的xy坐标,坐标原点即两线的交点。实验图像上准确标出坐标较难,就省略了。事实上,在x轴负向存在衍射光,图7中x轴向的强度曲线示于图8。



图9 直边衍射的实验测量与两种理论公式模拟的x轴向的强度曲线比较
理论模拟是将照明光视为理想均匀平面波,但实际上我们实验时的照明光没有理想均匀,因此,会出现实验图像的强度在x轴正向有增加的趋势。但对于衍射条纹的分布,我在计算机上移动鼠标,通过图像的像素数量比较。在鼠标移动时可分辨的范围内,衍射明暗条纹的理论模拟与实验测量吻合非常好。
下面两组实验就不再给出横向分布曲线了,此外,由于两种公式模拟的二维分布看不出什么区别,就都只用一个理论模拟图来表示。
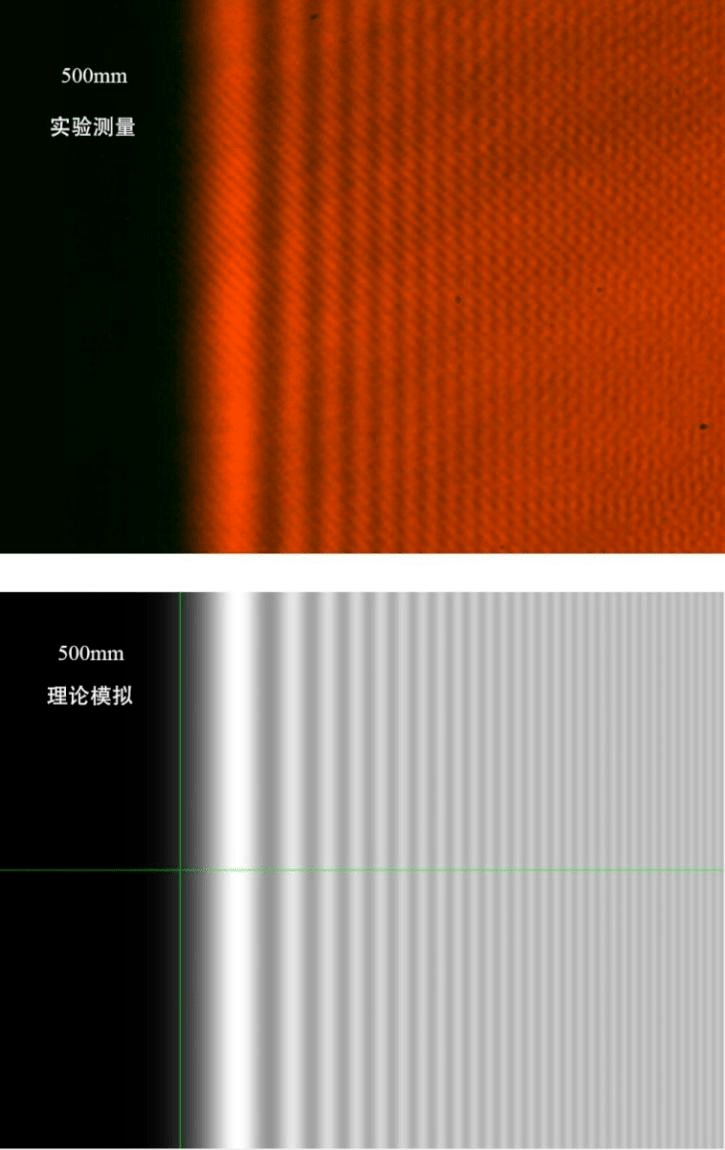
图10 衍射距离500 mm的直边衍射测量图像与理论模拟图像比较(图像宽度6 mm)
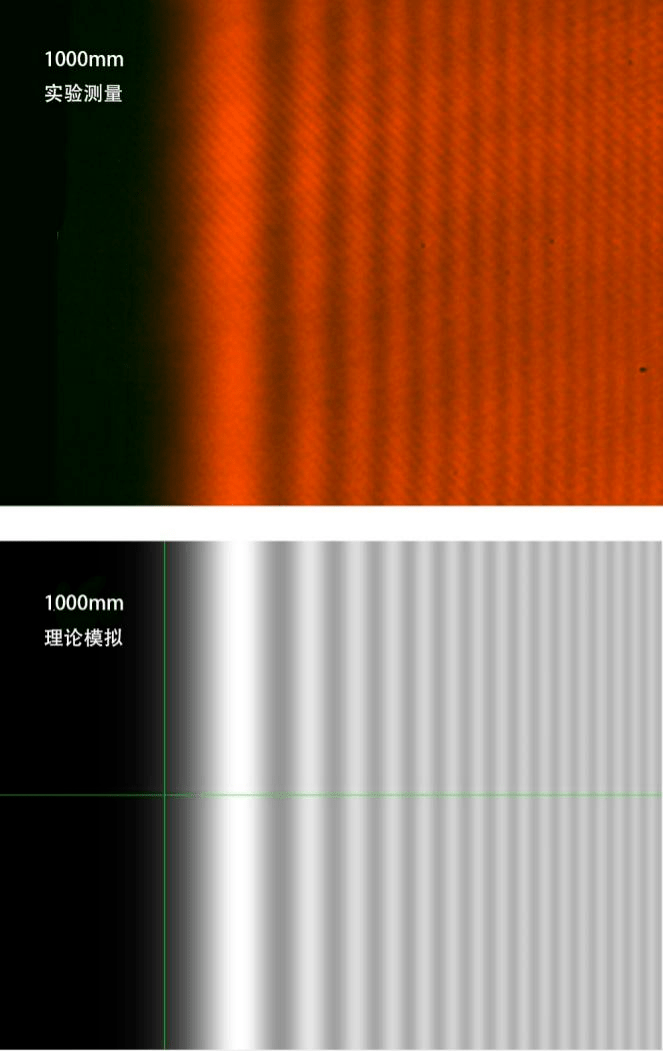
图11 衍射距离1000 mm的直边衍射测量图像与理论模拟图像比较(图像宽度6 mm)
(三)窄带光阑衍射
实验时用直径1 mm的钢丝进行的衍射实验,钢丝直径是我们用测微旋测量的。有可能钢丝的截面并不是准确的圆,估计实验时正对照明光的钢丝的宽度略小于1 mm,因此,用1 mm为直径的理论模拟衍射图像中央阴影区宽度略大,但条纹的分布形式与理论模拟吻合仍然很好,详见下面几个图像。
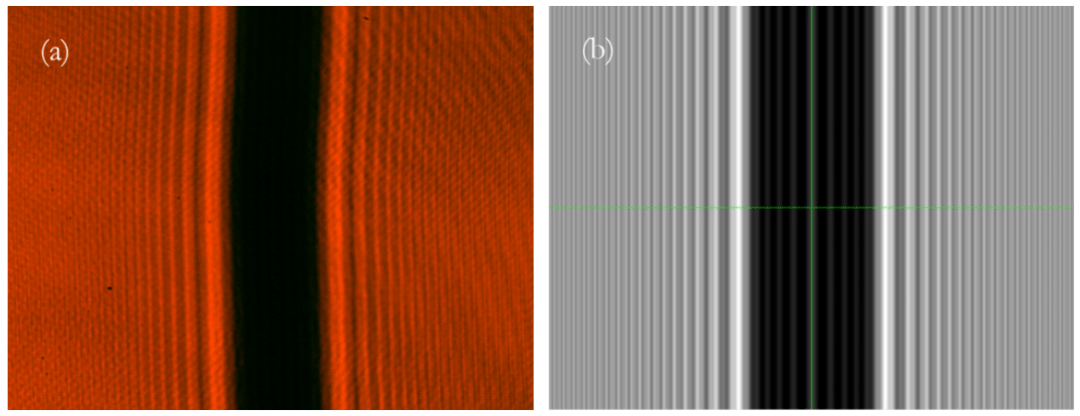
图12 衍射距离200 mm的钢丝衍射测量图像(a)与理论模拟图像(b)比较(图像宽度6 mm)
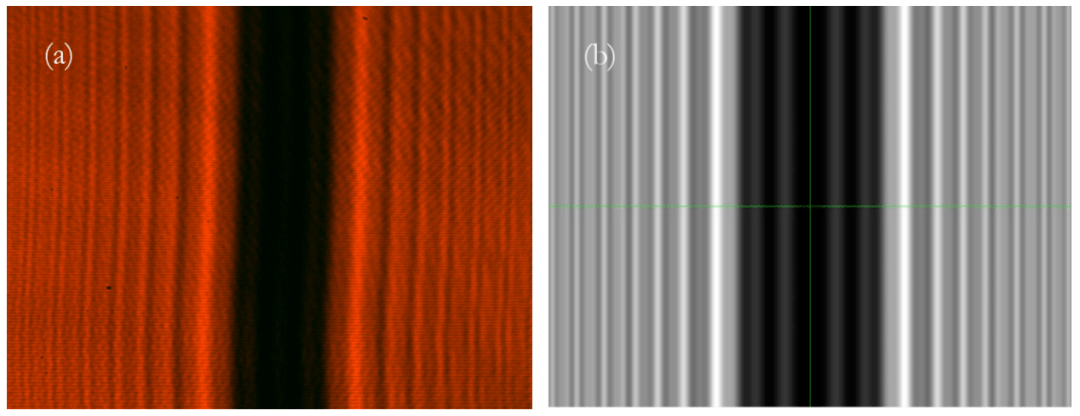
图13 衍射距离500 mm的钢丝衍射测量图像(a)与理论模拟图像(b)比较(图像宽度6 mm)

图14 衍射距离1000 mm的钢丝衍射测量图像(a)与理论模拟图像(b)比较(图像宽度6 mm)
虽然我们没有做狭缝衍射实验,但按照巴比涅原理,相信理论计算仍然能够得到与实验吻合的结果。
对于宽度为2 mm的方孔衍射,那天实验是用手机拍摄了由坐标纸记录的图像。由于照片中央斑的强度过饱合,模拟计算时我将强度大于最大强度1/50的区域均视为255进行显示,这样则较好地看出周边的衍射条纹。应该说,无论采用Siegman的计算公式或者是李老师导出的公式,理论计算均与实验测量相当吻合。

方孔宽度2 mm,衍射距离10 m,照明光波长6328 nm
图15 方孔衍射强度的实验测量与理论模拟的比较
樊老师交待的任务完成了,大家都很高兴,但又十分感叹:现在有了计算机,模拟计算菲涅耳衍射实验真方便。如果这些模拟计算也能用于实际,那该多好!
参考文献:
[1] [美]顾德门(Joseph. W. Goodman)著,陈家璧 等译,傅里叶光学导论[M](第4版),北京:科学出版社,2020年。P.90
[2] 李俊昌,激光的衍射及热作用计算[M],北京:科学出版社,2002:P.82.
[3] A. E. Siegman, Laser[M], University Science Books Mill Valley, California, 1986:P.719
[4] 李俊昌,熊秉衡,信息光学教程[M](第2版),北京:科学出版社,2017:P.37.
[5] Li Junchang C. Renard et J. Merlin, Etude théorique et expérimentales d'un dispositif optique de transformation de faisceau laser en une tache rectangulaire[J], Journal of Optics, vol.24, no.2, 1993, p.55-64.
李俊昌, C. Renard et J. Merlin, 一种将激光光束变换为矩形光斑光学装置的理论及实验研究[J],[法]光学, vol.24, no.2, 1993, p.55-64.
[6] 李俊昌, 激光热处理优化控制研究[M], 北京:冶金工业出版社,1995。
[7]Li Junchang,C. Renard et J. Merlin,Calcul des effets thermiques induits par un dispositif optique permettant de condenser un faisceau laser de puissance en une tache rectangulaire [J],Jounal de Physique III,France 3 (1993) p.1497-1508。
李俊昌,C. Renard et J. Merlin,大功率激光会聚为矩形光斑的一种光学装置的热作用计算[J],[法]物理III,no.3,1993,p.1497-1508。
预告:第十二篇 柯林斯公式及光学系统矩阵元素的实验测定
柯林斯公式是1970年由柯林斯(Collins S. A.)提出的,柯林斯将矩阵光学与菲涅耳衍射积分相结合,基于程函理论导出了这个公式。该公式可以准确地计算光波通过2×2光学矩阵描述的光学系统的衍射。2017年,光学名著《傅里叶光学导论》第4版介绍了柯林斯公式。作者寻思,如果该公式的提出时间早于1968年,顾德门(Joseph. W. Goodman)教授在《傅里叶光学导论》第1版无疑会对该公式进行介绍。这样,柯林斯公式现在必然是从事近代光学研究的科技工作者更为熟知而获得广泛应用的衍射计算式。
柯林斯公式的计算通常采用快速傅里叶变换进行,但计算前必须知道组成光学系统的所有部件的2×2光学矩阵元素。准确测量每一部件之间的间隔,按照光波通过光学系统的顺序,让所有部件及衍射空间光学矩阵作乘积运算才能获得光学系统的光学矩阵。当光学系统的部件较多时,确定每一光学部件的矩阵元素及准确测量每一部件间的距离是一件细致而繁杂的工作,容易形成累计误差,其误差将导致衍射计算误差。
为便于柯林斯公式的实际应用,下文基于光波通过光学系统的直边衍射条纹分布公式,提出通过衍射条纹较准确地测定光学系统矩阵元素的方法。并且介绍将矩阵光学与瑞利的衍射理论相结合,从另一途径导出柯林斯公式的数学过程。
/ 作者简介/

李俊昌,1945年生,汉族,昆明人,昆明理工大学物理光学二级教授。享受国务院特殊津贴、全国优秀教师、云南省优秀工作者、《中国激光》杂志常务编委(2008-2018)、云南书画院研究员、云南美术家协会会员。1968年毕业于云南大学物理系,1980年从工厂调入昆明理工大学任教至今。
作为客座教授,先后在法国里昂应用科技学院、法国里昂中央理工大学、法国巴黎高等工业大学、法国国家科研中心及法国缅茵大学合作科研或指导博士生。几十年来,在法国巴黎光学院等多所知名大学及国内中国科学院研究生院、清华大学、国防科技大学、西北工业大学、北京邮电大学、北京理工大学、北京工业大学、四川大学、成都光电所、上海光机所、香港城市大学及台湾师范大学等数十个知名科研院所进行过多次专题学术讲座。在物理光学领域的主要研究成果是修改了国内外50多年来一成不变的相干光成像近似理论。
第一作者在国内外著名学术期刊发表SCI及EI索引的科学研究论文60余篇,出版中、英、法文科学专著六部:1、《激光热处理优化控制研究》(冶金工业出版社1995年);2、《激光的衍射及热作用计算》(科学出版社2002年第一版,2007年修订版);3、《信息光学理论与计算》(科学出版社2009年);4、《信息光学教程》(科学出版社2011第一版,2017年第二版);5、法文专著《数字全息》Holographie numérique(法国巴黎:HERMES科技出版社2012年);6、《衍射计算及数字全息》(科学出版社2014年中文版,2016年英文版)。
自幼爱好书画,上世纪70-80年代,美术作品多次参加云南省美展,在报刊杂志出版过多种连环画。改革开放后主要从事科研及教学,但美术作品2019年及2021年入选云南省美展。
专栏文章:
菲涅耳的直边衍射条纹及泊松斑纹公式 | 李俊昌专栏⑥
半波带法及菲涅耳微波元法计算研究 | 李俊昌专栏⑦
菲涅耳衍射积分离散计算时的光场克隆研究 | 李俊昌专栏⑧
角谱衍射数值计算理论补充 | 李俊昌专栏⑨
菲涅耳函数的菲涅耳算法 | 李俊昌专栏⑩
中国激光杂志社招聘
工作地点:上海
1. 中/英文刊编辑
组稿、论文评审与期刊出版
2.出版编辑
稿件格式审核、编辑加工、校对
3.新媒体编辑
新媒体内容策划、生产、传播
点击了解详情
简历请发送至
zhouxiaoying@clp.ac.cn
邮件标题:应聘职位—姓名
End
首发前沿光学成果,放送新鲜光学活动
如需转载,请直接留言。
商务合作:季先生 18018304797
免责声明
本文中所出现的所有图片均为转载,如涉及版权等问题,请作者在20个工作日之内来电或来函联系,我们将协调给予处理(按照法规支付稿费或删除)。
最终解释权归《中国激光》杂志社所有返回搜狐,查看更多

