贞元的数学教育强调的是孩子思维的发展,而非机械的训练,这样的教育理念是如何在课程中具体落实的,来听一听七年级数学老师对于整式加减单元的教学随想。
从假期备课开始,整式加减这一章要怎么上就一直是萦绕在我心头的一个问题。
如果仅仅从知识与技能层面,这一章的东西真的很少:
概念就这么几个:
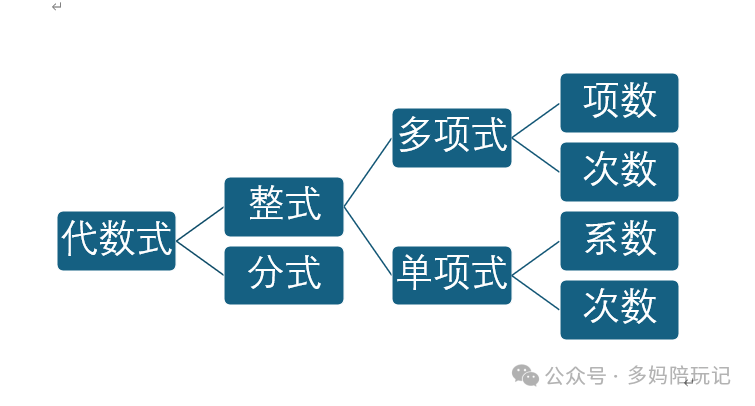
化简计算部分也没有任何新东西,都是运用有理数经验就可以了。看起来似乎很容易。
这一章涉及的考试题也不多,1)考概念,什么是单项式,什么是系数等等。2)考计算,多项式化简。如果以应对考试来进行这一章的教学,那真的找到几类典型题反复做就可以了。
但这一章是我认为孩子们要真正进入初中数学领域,最重要的一关。
很多孩子进入初中后都会突然觉得数学课听不懂了,用他们的话来说,变得“抽象”了。满黑板的符号,完全无法理解。
小学和初中数学最根本的不同在于对于思维抽象度要求的不同,小学阶段孩子们处于具体运算阶段,因此小学数学基本是用具体的数字和运算解决具体的问题。这些数字,运算,孩子们都是可见可感,甚至是可操作的。
而进入初中,孩子们将进入形式运算阶段,不再一个一个解决单独的问题,要开始运用代数一类一类去研究和解决问题。一类类解决问题最重要的是什么?1)你要能抽象出这类问题的关键要素,并用数学语言表示,这就是代数。2)你要能找到这些要素之间的规律与关系,并用数学语言描述,这就是我们说的建模,每一个代数式,本质都是一个数学模型。
那代数对于孩子们难吗?可能很多人会说小学阶段孩子们就学过代数了,比如孩子们知道周长公式是c=2(a+b),孩子们也学过简易方程,x-1=3。所以代数有什么难的?
的确,在教学中我们会发现,让孩子们用代数列出简单的数量关系对他们一点都不难。比如一件物品原价p元,8折出售,那现价是多少元?几乎所有孩子都能准确列出0.8p元。
是不是这样就以为孩子们已经拥有了代数思想,能用代数解决问题了呢?
不是的,能列出等量关系是因为孩子在小学有了充分的用具体的数解决问题的经验,他们把这个经验沿用到了初中,但是,孩子们真的理解这个p是什么意思吗?p在这里又意味着什么?我们为什么要用p呢?
整式这一章,孩子们第一个很大认知冲突就在于这些字母到底是什么?
p是字母还是数字?它可以是怎样的数字?这个代数式还可以解决其他问题吗?在课堂上每一个基于实际问题的代数式,我都不断追问这3个问题,不断让孩子感受,p是任意一个数,在实际情境中因为是价格,它会是大于0的任意一个数,这个代数式对于任何产品打八折销售的现价都适用。
为什么要这样问?就是要逼孩子们突破具体数解决问题的思维惯性,充分理解代数到底“代”什么?这么“代”有什么好处?本质上就是让他们理解抽象的代数,并且建立用代数一类类解决问题的模型意识。
那这样就够了吗?
对于实际情境中理解代数式有了充分的讨论,我会发现一旦脱离实际情境,孩子们对于代数的理解又会被表面假象所欺骗。
比如孩子们依然认为,a是一个整数,-a是一个负数,a+1一定大于1。
孩子们知道2x3+3=(2+1)x3, 但面对下面式子的时候,就会这样处理。
这里的错误原因不是孩子没有记住整式化简的法则(如果他理解了代数本质,法则根本不需要记),而是孩子们还无法脱离情境把代数当成一个数来看。如果不能让孩子突破这一点,单单要求孩子去背诵整式化简的法则,这对孩子的数学思维不仅没有任何发展,反而是一个巨大的伤害
因此,孩子们对于代数可以指代任意有理数(现阶段)的观念只能基于实际情境理解,还不能从抽象层面真正领会。怎么办呢?
我想到了在有理数章节,我们研究了具体的有理数的运算,相反数,绝对值,幂运算。当时是基于具体的数进行研究的,那现在,在学习了代数后,我们是否能从代数层面对有理数章节这些内容做一个代数层面简单且清晰的梳理,也通过梳理帮助孩子们脱离实际情境去理解代数的本质。
于是在原有的课程设计基础上,增加了三节综合课, 包括:
1)用代数思维研究绝对值和相反数。在有理数单元上|a|的时候,孩子们对于这个a非常困惑,而现在经历了代数章节的学习,孩子们对于a的认识明显比当时好了很多,但是对于a以及a的各种变式(a+1,-a,-a-1)同样也是代数,同样也能代表任何数的抽象还不够,因此在这节课上重点对于这一层认知冲突的突破做了讨论。
2)用代数思维自己总结并表述有理数加减乘除的规律,我们在教学的时候让孩子去理解算例,并没有让孩子背诵法则。在这里目的也不是让孩子去背法则,而是让孩子们用代数思维去总结规律,感受代数的本质就是数,并且代数能非常简洁清晰说明一类问题。背后体现从特殊到一般,用代数思维去发现规律并且表达规律解决问题的全过程。所谓的规律,就是一种模型,找规律的过程就是建模的过程。
3)用代数思维去找规律。这节课也是让孩子从特殊数到一般化的代数去寻找规律。有孩子在这节课的挑战单后问了一个非常好的问题,我们发现这些规律有什么用?通过讨论,希望让孩子们感受到我们并不是要去研究如何做这些规律题,而是要去体验如何从特殊到一般去发现规律并描述规律的思维过程。用代数思想发现并表达现实生活规律在生活中非常重要,餐厅怎么决定每天备多少食物,天气预报,股票走势等,生活中的万事万物都蕴含着规律,而代数就是能把最本质的要素和关系抽象出来,清晰表达出事物规律,帮助我们更好的认识世界并形成决策的一种思想武器。
左边是我们曾经一个个去研究的问题,而右边是我们现在有了代数武器后,一类类去研究的问题。这是我们从小学数学到初中数学,思维的巨大飞跃。这是代数这一章最根本的核心和意义。

只有把握好了代数这一层的意义,真正建立起用代数去描述和表达问题的抽象思维,孩子们才能在未来开始进入方程,不等式,函数这三个初中代数核心领域的研究。不然,孩子们在初中的数学课,就会越上越抽象,越上越不知所云。
当然,不是上了课,孩子们就一定构建好了代数观念。思维的构建需要时间,每个孩子思维发展也会有差异,整个初中数学,从代数开始,到后面方程函数不等式,都是在围绕这样一个思想进行数学研究。我们一定不能要求孩子一步登天,一说就懂,从埋下种子到发出小芽到长成大树,给予足够的时间来浇灌。返回搜狐,查看更多

