来源:网络
《长方体表面积》挖块问题(不挖通)
①从顶点角挖去
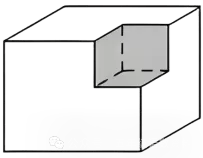
表面积:去掉3个面,又露出3个面,
表面积不变。
例 题:在一个棱长为4厘米的正方体的一个顶点处挖掉一个棱长为1厘米的小正方体,那么剩余部分的表面积是多少?
表面积不变:4×4×6=96(cm²)
②从中间挖去
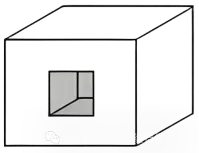
表面积:去掉1个面,又露出5个面,
原有表面积增加4个面的面积。
例 题:在一个长为5厘米,宽为4厘米,高为3厘米的长方体前面正中间挖掉一个棱长为1厘米的小正方体,那么剩余部分的表面积是多少?
原本的表面积:(5×4+5×3+4×3)×2=94(cm²)
增加的表面积:1×1×4=4(cm²)
现在的表面积:94+4=98(cm²)
③从棱边上挖去

表面积:去掉2个面,又露出4个面,
原有表面积增加2个面的面积
(即左、右两个面)。
例 题:在一个棱长为5厘米的正方体的一条棱上挖掉一个棱长为2厘米的小正方休,那么剩余部分的表面积是多少?
原本的表面积:5×5×6=150(cm²)
增加的表面积:2×2×2=8(cm²)
现在的表面积:150+8=158(cm²)
《长方体表面积》组合问题
1.将2个棱长为2厘米的小正方体拼成一个长方体,它的表面积减少多少平方厘米?拼成的长方体表面积是多少?

如图:拼起来后,减少了2个面
减少:2×2×2=8(平方厘米)
长方体:2×2×12-2×2×2=40(平方厘米)
答:表面积减少8平方厘米,拼成的长方体表面积40平方厘米。
2.将3个小正方体拼成一个长方体,它的表面积减少了20平方厘米,求一个正方体表面积是多少平方厘米?

如图:拼起来后,减少了4个面正好减少了20平方厘米。
正方体:20÷(2+2)×6=30(平方厘米)
答:正方体表面积是30平方厘米。
3.用4个棱长都是2厘米的正方体拼成一个长方体,长方体的表面积与原来的4个正方体的表面积之和相比表面积最多减少多少平方厘米?最少减少多少平方厘米?

拼成的长方体有两种情况:
最少:2×2×(2+2+2)=24(平方厘米)
最多:2×2×(2+2+2+2)=32(平方厘米)
答:最少减少24平方厘米,最多减少32平方厘米。
《长方体表面积》切割问题
平切:增加两个面(两个上面或两个下面),
增加的面积之和=长×宽×2
横切:增加两个面(两个前面或两个后面),
增加的面积之和=长×高×2
纵切:增加两个面(两个左面或两个右面),
增加的面积之和=宽×高×2
1.将一个长6cm,宽2cm,高2cm长方体切成3个正方体,增加了几个面?3个正方体的表面积之和比长方体的表面积增加了多少平方厘米?
增加面:2+2=4(个)
增加表面积:2×2×4=16(平方厘米)
答:增加了4个面,增加表面积16平方厘。
2、一个正方体的表面积是54平方厘米,将它平均分成两个小长方体,表面积增加了多少?
分析:正方体表面积是六个大小相同的正方形的面积之和,把正方体平均分成两个长方体,只需要切一刀,增加两个大小相同的正方形面。
增加表面积:54÷6×2=18(平方厘米)
答:表面积增加了18平方厘米。返回搜狐,查看更多

